|
5.2 Periodic Functions
A periodic function can be defined as any function for which,
f (t) = f (t + T) ......(i) for all t.
The smallest constant T which satisfies (i) is called the period (or the fundamental period)
of the function.
By iteration of (i), we have
f(t) = f (t + nT), n = 0, ± 1, ± 2, ±3, ....... (ii)
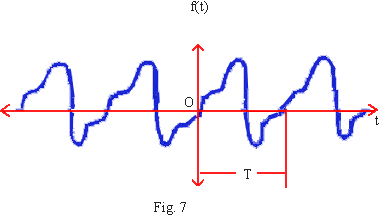
An example of a periodic function is shown in fig. 7
A very simple but interesting case we can observe from the unit circle. Its circumference is
2pr, but r = 1 \ C = 2p. If any point P moves around it for a distance of
2p, it returns to where it started. In other words, for any value of 't' if
2p is added or subtracted, P(t) has the same coordinates.
(1) From this discussion it follows that,
sin (t +2p) = sin t
sin (t - 2p) = sin t
cos (t + 2p) = cos t
cos (t - 2p) = cos t
If 'n' is an integer sin (t + 2np) = sin t
cos (t +
2np) = cos t
\ sine and cosine functions have the property as given in (ii). Therefore sine and cosine
functions are 'periodic functions'. Also we note that no real number less than
2p can be made of period of sine and cosine functions. Therefore
'2p' is the 'fundamental period' of sin t and cos t.
(2) Let us now consider tan t, t Î R, cos t
¹ 0
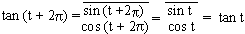
\ tan t is periodic and periodic with period
2p
We further observe that, 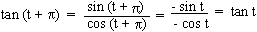
p is also period of tan t. Since p < 2p, the fundamental period of tan t cannot be
2p.
|