|
EXAMPLE 5
Find the period of f (t) = 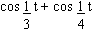
Solution : If f (t) is periodic with period T then,
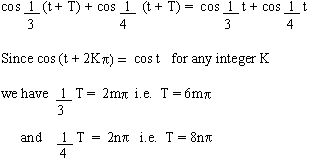
where m and n are integers.
Therefore T = 6mp = 8np
When m = 4 and n = 3, we get smallest value of T (by trial and error method)
Hence T = 24p
In general, if the function
f (t) = cos w1t + cos w2t is periodic with
period T then w1T = 2mp and w2T = 2np Þ
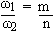
i.e. w1 / w2 must be a rational number.
EXAMPLE 6
Is the function f (t) = cos 10 t + cos (10 +
p )t periodic ?
Solution :
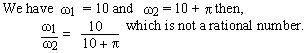
Therefore we cannot find T. Hence f(t) is not periodic.
EXAMPLE 7
Find the period of the function f(t) = (5 cos t)2
Solution :
We know that cos2x = 1/2 (1 - cos2x)
We have f(t) = (5 cos t)2 = 25 cos2t
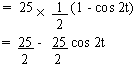
Since if f (t) = K, constant function then
f (t+ T) = K = f (t) \ f (t) is periodic for any T
and cos 2t is periodic with period p.
|