|
EXAMPLE 1
Is the function f(x) = 4x4 + x2 even, odd or neither?
Solution : f(x) = 4x4 + x2
\ f(-x) = 4(-x)4 + (-x)2
= 4x4 + x2
= f (x)
Since f (-x) = f (x), the function is even.
Note : An even degree polynomial function of one variable is always an even function.
EXAMPLE 2
Is the function f(t) = 5t5 - 7t3 - t even, odd or neither?
Solution: f(t) = 5t5 -
7t3 + t
\ f(-t) = 5(-t)5 -
7(-t)3 - (-t)
=
-5t5 + 7t3 + t
= -
(5t5 - 7t3 -t)
= - f (t)
Since f(-t) = -f (t). The function is odd.
EXAMPLE 3
Find f (t) + f (-t) if f (t) = 3t3 + 2t - 4sin t
Solution : f (t) = 3t3 + 2t - 4 sin t
\ f (-t) = -3t3 - 2t + 4 sin t
\ f (t) + f (-t) = 0
EXAMPLE 4
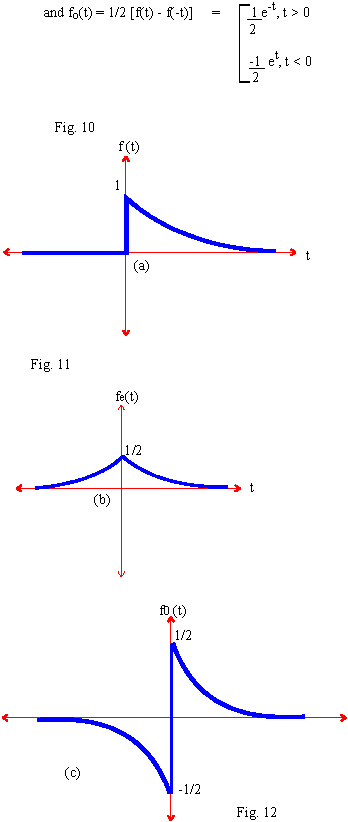
Find the even and odd components of f(t), defined as,
f(t) = 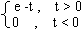
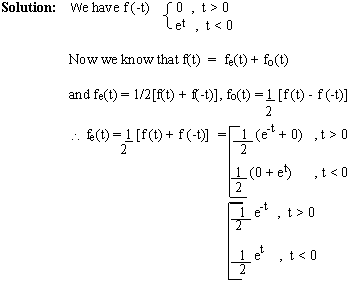
|