|
Complex Number
Let us consider a quadratic equation say, x2
- 2x + 5 = 0. Hence the discriminant b2 - 4ac, being
negative, it leads to the solution set { 1 - 2i, 1 + 2i}. The roots
viz x = 1 - 2i and x = 1 + 2i is that they are partly real and partly
imaginary. We now introduce a number which is a combination of real
and imaginary numbers. This is called a Complex number of the type
a + bi , a, b Î R. We denote this by z then
z = a + ib ...........(ii)
Here a = R (z) ...... real part z and b = I (z) ..... imaginary
part z.
The same may be expressed more elegantly as an ordered pair of
two real numbers a and b as,
z = (a , b) ..........(iii)
For example, z1 = (2, 3) = 2 + 3i,
z2 = (2, -3) = 2 - 3i,
z3 = (0, 1) = 0 + i = i ,
z4 = (0, 0) = 0 + 0i = 0
which is a real number = 0
Conjugate Complex : If z = a + bi is a complex number then
z or z* = a - bi is called conjugate complex of z.
For example, z1 = 3 + 2i then 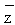 1
= 3 - 2i, 1
= 3 - 2i, 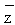 2
= - 8 - 4i then z2 = - 8 + 4i. 2
= - 8 - 4i then z2 = - 8 + 4i.
Basic Operations : From the point of view
of an axiomatic foundation, it is advised to treat a complex as
an ordered pair (a,b), a, b Î R; subject to certain operational
rules.
Equality of two complex numbers : Let z1
= (a,b) and z2 = (c,d) then z1 = z2
iff a = c
and b = d.
Sum : Let z1 = (a,b) and z2
= (c,d) then z1 + z2 = (a + c, b + d )
Difference : z1 - z2
= (a - c, b - d)
Product : z1 . 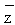 = (a, b) (c,d) = (ac - bd, ad + bc)
= (a, b) (c,d) = (ac - bd, ad + bc)
Scalar Multiplication : kz = (ka, kb) if
k is a scalar and z = (a,b)
Quotient : 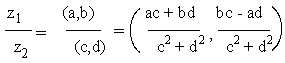
Product of conjugate complexes : z . z = (a + bi)
(a - bi) = a2 + b2
Closer Property : From the operations between
any two complex numbers is again a complex number only. As such
we remark that the set 'C' of complex numbers is closed with respect
to these operations.
[next page]
|