Geometrical Representation :- Consider a system of 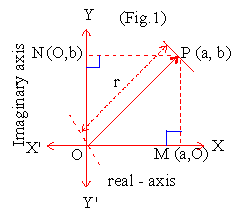rectangular co-ordinate axes X ' OX and Y ' OY. Then each complex number z = (a,b) corresponds to a point P º (a,b) and conversely to every point on XY -plane there corresponds a complex number. Any number of kind M º (a,O) is a point on x-axis and N º (O,b) is a point on y-axis. Hence X-axis is called the "real axis" and Y-axis is called the "imaginary axis". Such a representation is called the "Argand's diagram" due to J.R.Argand and XY plane is called Argand's plane.

(A) MODULUS : From the fig. OP = r =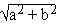

If z = (a,b) is a complex number then r = | z | =

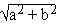
is called its modulus \ | a + bi | =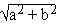

For example, | 3 + 4i | = 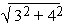= 5, | 5 - 12i | = 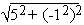= 13

(B) Argument or Amplitude : If OP makes angle q with 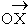, then q is called the "argument or amplitude" of the complex number z = (a,b)

From the right triangle OPM, we get

OM = a = r cos q ..... (i) and ON = b = r sin q ....(ii)

So that r = 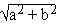and tan q = 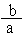\ q = tan-1 (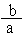) = argument z

Thus if q satisfies simultaneously the relations

cos q = 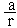= 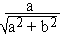and sin q = =

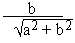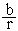
and that - p £ q £ p is called the argument or the amplitude of the complex number z = (a, b)

Polar Form

Using the above relations i.e. a = r cos q and b = r sin q

then z = a + bi = r cos q + i (r sin q)

\ z = r (cos q + i sin q) ...... This is called the polar form of the complex number z.

Note that by Eular's formula i.e.

e^iq = cos q + i sin q we get z = r (cos q + i sin q ) = r e^iq

This is known as the exponential form of the complex number.

Example 1

Evaluate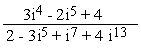

Solution

Now i⁴ = (i²)² = (-1)² = 1, i⁵ = i⁴´ i = (1) i = i

and i⁷ = i⁶´i = (i²)³ . i = (-1)³ . i = - i , i¹³ = i¹² ´ i = (i²)⁶ . i = (-1)⁶. i = i

\

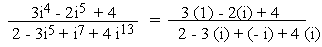
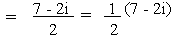
[next page]

Index

8.1 Geometry of complex numbers
8.2 De - Moivres's theorem
8.3 Roots of complex numbers
8.4 Cirsular functions of complex angles & hyperbolic function
Supplementary Problems

Chapter 9