Example 3

Solution

x⁹ - x⁵+ x⁴ - 1 = x⁵ (x⁴ - 1) + 1(x⁴ - 1) = (x⁵+ 1) (x⁴ -1)

Now the 1st factor,

x⁵ + 1 = 0 Þ x⁵ = -1 = cos (2k + 1) p + i sin (2k + 1)p

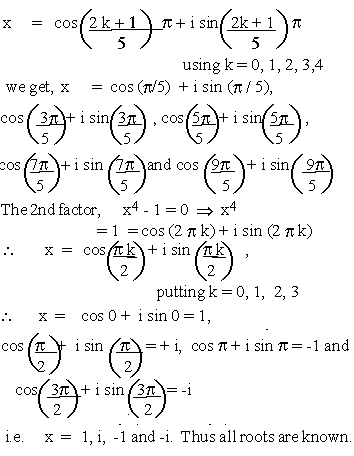
Example 4

Solve x¹² - 1 = 0 and which of its roots satisfy the equation x⁴ + x² + 1 = 0

Solution

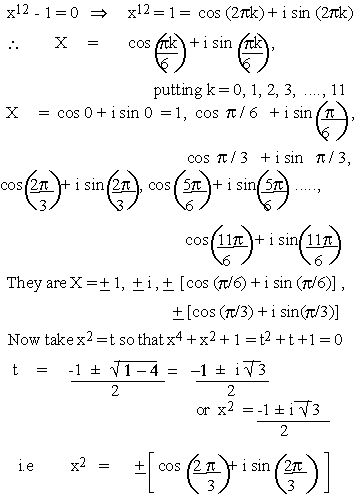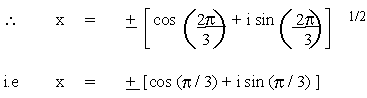
Therefore these roots satisfy both x¹² - 1 = 0 and x⁴ + x²+ 1 = 0

Example 5

If a and b are roots of x² - 2x + 4 = 0. Find aⁿ + bⁿ. Hence a¹⁵ + b¹⁵

Solution

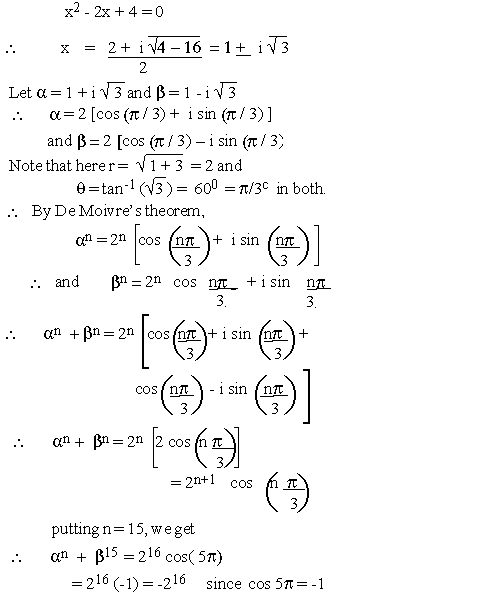
Example 6 Find all values of (1 + i)^1/3and represent them on the Argand's diagram.

Solution

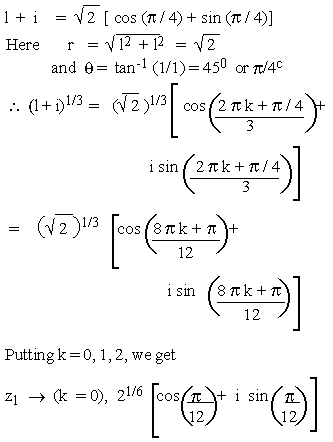
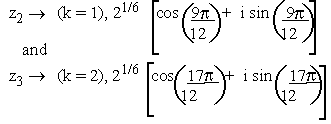
Thus z1 , z2 and z3 are the required all values of (l + i)1/3

They are represented on the Argand's diagram as

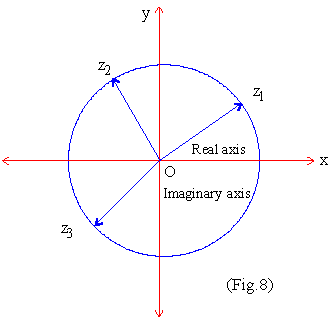
[next page]

Index

8.1 Geometry of complex numbers
8.2 De - Moivres's theorem
8.3 Roots of complex numbers
8.4 Cirsular functions of complex angles & hyperbolic function
Supplementary Problems

Chapter 9