1. The normal curve is bell-shaped and symmetrical about the maximum ordinate at x = m, the mean. This ordinate divides the curve into two equal parts. The part on one side is the mirror image of the other side. it has the maximum height at x = m. Thus the mode of the distribution is also m. The ordinate x = m divides the whole area under the curve into two equal parts. Hence the median is also x = m. Thus for the normal distribution, the mean, mode and median coincide. i.e. mean = median = mode = m.

2. We know that the area under the normal curve is equivalent to the probability of randomly drawing a value in the given range. The area is the greatest in the middle, where the "hump" (where mean, mode and median coincide) and then thin out towards out on the either sides of the curve, i.e. tails, but never becomes zero. In other words, the curve never intersects x-axis at any finite point. i.e. x-axis is its Asymptote.

3. Since the curve is symmetrical about mean. The first quartile Q₁ and the third quartile Q₃ lie at the same distance on the two sides of the mean m. The distance of any quartile from m is 0.6745 s units. Thus,



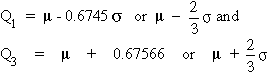
Hence, middle 50% observations lie between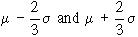

4. Since the normal curve is symmetrical its skewness is zero and kurtosis is 3. The curve is meso kurtic.

5. The mean deviation is 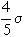approximately.

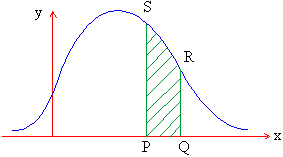
6. As discussed earlier, the probability for the variable to lie in any interval ( a, b ) in the range of variable is given by the are under the normal curve, the two ordinates x = a and x = b, and the x-axis.

[next page]

Index

7. 1 Introduction
7. 2 Trial
7. 3 Sample Space
7. 4 Definition of Probability
7. 5 The Laws of Probability
7. 6 Conditional Probability
7. 7 Theoretical Distribution
7. 8 Binomial Distribution
7. 9 Normal Distribution

Chapter 8