Measure of an angle : Every angle has a measure. It is measured in degrees from 0⁰ to 180⁰ and is represented as m Ð. A line is also an angle because it satisfies the definition of having two rays going in different ( in this case opposite ) directions with a common end point ( figure 1.14 ).

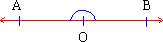
Figure 1.14

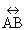is also Ð AOB and m Ð AOB = 180⁰

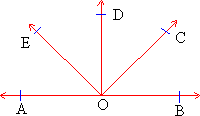
Figure 1.15

All rays starting from O and going above line AB form angles with 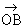such that their measure is between 0⁰ and 180⁰. eg. Ð COB , Ð DOB and Ð EOB.

Angle addition property : Two angles with a common side and a common vertex are adjacent if their interiors are disjoint . The measures of two adjacent angles can be added to find the measure of the resultant angle. This is called the angle addition property. With reference to figure 1.15 m Ð COB + m Ð DOC = m Ð DOB.

Angle Bisectors : The ray which passes through the vertex on an angle and divides the angle into two angles of equal measure is called the bisector of that angle. Of the two angles ( figure 1.16 ) Ð AOB and Ð COB are equal in measure then 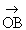is called the bisector of Ð COA. Just as every line has only one midpoint every angle has only one bisector.

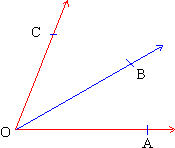
Figure 1.16

Index

Introduction

1.1 Points, Lines and Planes
1.2 Line Segment
1.3 Rays and Angles
1.4 Some Special Angles
1.5 Angles made by a Transversal
1.6 Transversal Across Two Parallel Lines
1.7 Conditions for Parallelism

Chapter 2