5.2 Ratio and Proportionality
Ratio is a comparison of two numbers expressed in the simplest fraction form. If a city covers an area of 100 square miles and another city covers 200 square miles, the 'ratio' of their area is expressed as 100 : 200 or on simplification 1 : 2. This means that the second city is twice as large as the first.
Ratio is a very useful way of comparing two numbers. If the age of the father is 50 years and that of the son is 10 years the ratio of their ages is 50 :10 or 5 : 1 which means that the father is five times the sonís age.
If in a linear pair the ratio of angles is 1 : 2, it is possible to find the exact measure of both the angles. If the measure of the smaller angle is x, the measure of the bigger angle is 2x. Therefore x : 2x = 1 : 2.
Since a linear pair of angles sum upto 1800
x + 2x = 1800
3x = 1800
x = 600
\ 2x = 1200
The two angles are 600 and 1200
Proportionality : Compare the drawing of
a bridge on a paper with the actual structure. They look similar
because the ratios of height to width to length are the same in
both the cases.
The equation which shows that two ratios are equal is called proportion. The design on paper and the actual structure look the same because they are proportionate to each other.
Equality in ratios is expressed as follows :
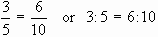
The number at the end i.e. 3 and 10 are called extremes and the numbers in the middle are called means.
Proportions have four properties.
1) Cross Product Property
If 
This is also called the cross multiplication property.
2) Switching or exchange property.
If 
3) Upside down or inverting property.
If 
4) Denominator addition or substraction property.
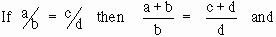
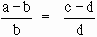
Example 1
A segment measuring 10 cm is divided into two parts in the ratio 1 : 3. What is the length of each part ?
Solution:
Let the length of one part of the segment be x then that of the other will be 3x .
Given that x + 3x = 10 cm.
or
4x = 10 cm.
\ x = 2.5 cm.
Therefore one segment measures 2.5 cm. and the other 7.5 cm.
[next page]
|