5.6 Similar Triangles
Two triangles are similar if their corresponding angles are congruent and their corresponding sides are proportional. It is however not essential to prove all 3 angles of one triangle congruent to the other, or for that matter all three sides proportional to the other. Out of these if some particular conditions get satisfied the rest automatically get satisfied. Those particular conditions would be sufficient to ensure similarity. A group of sufficient conditions is called as a test for similarity. These tests are based on two basic principles.
1) In 2 triangles if the corresponding angles are congruent, their corresponding sides are equal.
2) If the sides of 2 triangles are proportional then the corresponding angles are congruent.
A - A Test: If two angles of one triangle
are congruent with the corresponding two angles of another triangle,
the two triangles are similar.
The sum of all three angles of a triangle is 1800. Therefore if two angles are congruent the third is automatically congruent. Therefore the sufficient condition requires only two angles to be congruent.
S A S Test: If two sides of one triangle
are proportionate to the two corresponding sides of the second triangle
and the angles between the two sides of each triangle are equal
the two triangles are similar.
S S S Test: If the three sides of one triangle are proportional
to the three corresponding sides of another triangles, then two
triangles are similar.
Example 1
D ABC and D
DEF have a one to one correspondence such that
l
(seg.AB) = 6 l
(seg.DE) = 3
l
(seg.AC) = 8 l
(seg.DF) = 4
l
(seg.BC) = 10 l (seg.EF)
= 5. Are the two triangles similar ? If so, why ?
Solution:
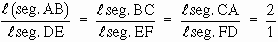
Yes. The two triangles are similar because their corresponding sides are proportionate.
[next page]
|