|
Thus it is proved that the measure of the inscribed angle is half
that of the intercepted arc.
Theorem: If two inscribed angles intercept the same arc or arcs of equal measure then the inscribed angles have equal measure.
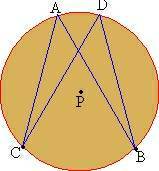
Figure 7.7 In figure 7.7 Ð
CAB and Ð CDB intercept
the same arc CXB.
Prove that m Ð
CAB = Ð CDB.
From the previous theorem it is known that
m Ð
CAB = 
m (arc CXB) and also
m Ð CDB =
m
(arc CXB)
\
m Ð
CAB = m Ð CDB
Therefore if two inscribed angles intercept the same arc or arcs of equal measure the two inscribed angles are equal in measure.
Theorem: If the inscribed angle intercepts
a semicircle the inscribed angle measures 900.
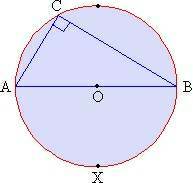
Figure 8.8 The inscribed angle Ð
ACB intercepts a semicircle arc AXB (figure 8.8). We have to prove
that m Ð ACB
= 900.
m Ð ACB =
m (arc AXB)
= (1800)
=
900
Therefore if an inscribed angle intercepts a semicircle the inscribed angle is a right angle.
Example 1
a) In the above figure name the central angle of arc AB.
b) In the above figure what is the measure of arc AB.
c) Name the major arc in the above figure.
Solution:
a) Ð AOB
b) 800. The
measure of an arc is the measure of its central angle.
c) Arc AXB
Example 2
a) In the above figure name the inscribed angle and the intercepted arc.
b) What is m (arc PQ)
Solution:
a) inscribed angle - Ð
PRQ
intercepted arc - arc PQ
b) 600. The
measure of an intercepted arc is twice the measure of its inscribed
angle.
Example 3
Ð PAQ and Ð
PBQ intercept the same arc PQ what is the m Ð
PBQ and m (arc PQ) ?
Solution:
m Ð
PBQ = 400
If two inscribed angles intercept the same arc their measures are
equal m (arc PQ) = 800
as m (arc) = 2m (inscribed angle).
|
