1. The values of mean, median and mode do not coincide. The more the difference between them, the more is the skewness.

2. Quartiles are not equidistant from the median. i.e. ( Q₃ -Me ) ¹ ( Me - Q₁ ).

3 The sum of positive deviations from the median is not equal to the sum of the negative deviations.

4. Frequencies are not equally distributed at points of equal deviation from the mode.

5. When the data is plotted on a graph they do not give the normal bell-shaped form.

1. First measure of skewness           It is given by Karl Pearson

Measure of skewness                     Co-efficient of skewness

Skp = Mean - Mode                               J =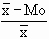

i.e. Skp =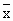 - Mo

Pearson has suggested the use of this formula if it is not possible to determine the mode (Mo) of any distribution,

( Mean - Mode ) = 3 ( mean - median )

Skp = 3 ( 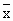- Mo ) Thus J =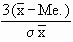

Note : i) Although the co-efficient of skewness is always within ± 1, but Karl Pearson’s co-efficient lies within ± 3.

ii) If J = 0, then there is no skewness

iii) If J is positive, the skewness is also positive.

iv) If J is negative, the skewness is also negative.

Unless and until no indication is given, you must use only Karl Pearson’s formula.

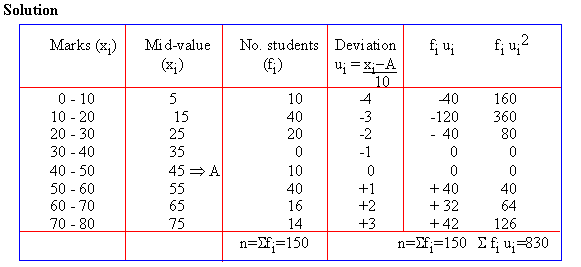
Example Find Karl Pearson’s coefficient of skewness from the following data:

[next page]

Index

5.1 Introduction
5.2 Methods of computing dispersion
5.3 Range
5.4 Mean Deviation
5.5 Variance
5.6 Coefficient of Variation
5.7 Percentile
5.8 Quartiles and interquartile range
5.9 Skewness moments and Kurtosis
5.10 Kurtosis

Chapter 6