|
For frequency distribution,
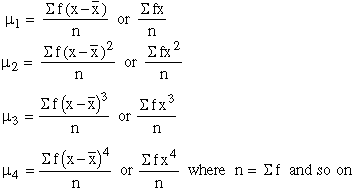
In many cases it is very difficult to calculate moments about actual moment, particularly when actual mean is in fractions. In such case we first compute moments about an arbitrary origin ’A’ and then convert these moments into moments about actual mean. These are called ’ raw moments ’ which are denoted by n.
Thus we have
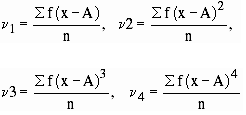
and so on. For frequency distribution
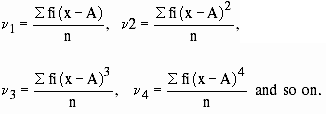
Now to obtain the central moment as
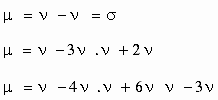
Pearson’s b and n coefficients. Karl Pearson defined the following four coefficients, based upon four moments about the mean.
b
coefficients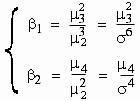 
n
coefficient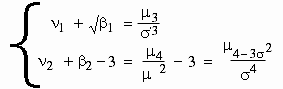 
These are pure numbers and they provide information about the shape of the curve obtained from the frequency distribution.
For symmetrical distribution, the moments of odd order about
the mean vanish and therefore m3
= 0 rendering b1 = 0 thus
b1 gives the measure of departure
from symmetry and also defines a measure of skewness. Also b2
= 
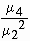gives the measure of flatness of the mode and also defines the measure
of Kurtosis or convexity of the curve.
Note : 1) If b2
= 3 i.e. n2 = 0 then the curve
is normal which is neither flat nor peaked i.e. Meso kurtic.
2) If b2
> 3 i.e. n2 > 0 then
the curve is more peaked than a normal curve and is called Lepto
kurtic.
3) If b2 < 3 i.e. n2 <> 0 then curve is flatter than a normal curve and is called Platy kurtic.
**********
[next chapter]
|
