|
Trigonometric Point
Let 't' be any real number. Start from point A(1, 0) on the unit circle and measure along
its circumference an arc of length | t | units. If t
³ 0, measure the arc length in the counter
clockwise direction; if t < 0, measure the arc length in the clockwise direction.
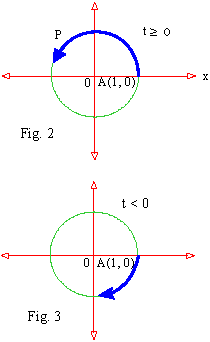
In this way we get a unique point on the unit circle (see fig 2,3). If this point is named as
P, then P is a trigonometric point and we donate if by P(t) and we say that P(t) is a
trigonometric point of the real number 't' which sets up an ordered pair. The corresponding relation
between 't' and P(t) defines a function whose domain is the set of real numbers and range is
the set of points on the unit circle. This function (circular function) is the set of ordered pairs
of numbers [t, P(t)].
Some of these ordered pairs can be found easily.
(i) For t = 0; P(t) = P(0) then the trigonometric point is A
º (1,0)
(ii) For 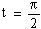 i.e. 90 0 which is
i.e. 90 0 which is 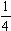 (circumference), then
(circumference), then
P(t) = P  is the trigonometric point B
º (0, 1) is the trigonometric point B
º (0, 1)
(iii) For t = p = 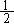 (circumference), then P (t) =
P(p) is A' º (-1,0) and (circumference), then P (t) =
P(p) is A' º (-1,0) and
(iv) For 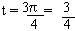 (circumference), then P(t) = (circumference), then P(t) =
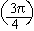 is B' º (0,-1), By reasoning, (2p)
is again Aº (1,0), P is B' º (0,-1), By reasoning, (2p)
is again Aº (1,0), P  is
B'º (0, -1),
and P (-p) is A'º(-1, 0) and P is
B'º (0, -1),
and P (-p) is A'º(-1, 0) and P 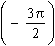 is B
º (0,1) is B
º (0,1)
|
Index
5.
1 Circular function
5.
2 Periodic function
5.
3 Even & Odd
5.4
Graphs of Trigonometric Functions
Supplementary
Problems
Chapter 6
|