|
To locate 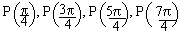 we reason as follows. Let P (t) be the ordered
pair P(x,y). For every value of 't' the point P(t) is on the unit circle. Therefore, if one of
the coordinates of P(t) is known, using x 2 + y2 = 1, we can find the other coordinate (except
for sign). we reason as follows. Let P (t) be the ordered
pair P(x,y). For every value of 't' the point P(t) is on the unit circle. Therefore, if one of
the coordinates of P(t) is known, using x 2 + y2 = 1, we can find the other coordinate (except
for sign).
From the plane geometry, P 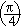 is the midpoint of arc AA' which is equidistant from
x
and y axes so that x = y (see fig. no. 3) is the midpoint of arc AA' which is equidistant from
x
and y axes so that x = y (see fig. no. 3)
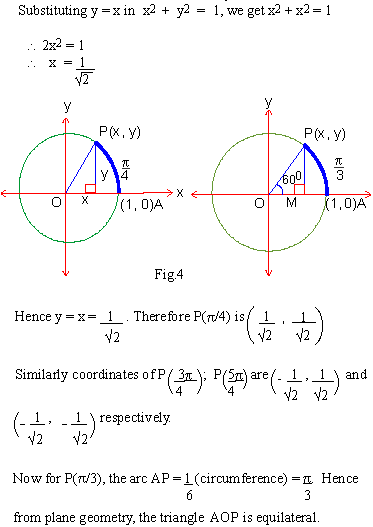
Construct PM perpendicular to OA. Then, from school geometry OM= 1/2 OA but OA = 1.
Therefore OM = 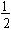 (See fig. no. 4) (See fig. no. 4)
Hence x = 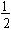 using x2 + y2 = 1 using x2 + y2 = 1
(1/2)2 + y2= 1
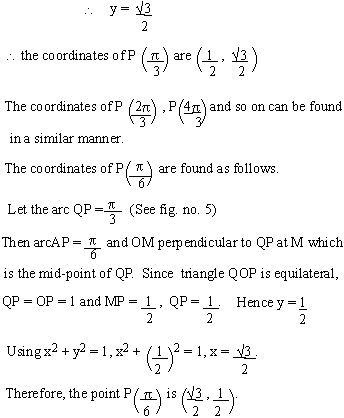
The coordinates of 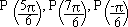 and so on, can be obtained without too much difficulty. and so on, can be obtained without too much difficulty.
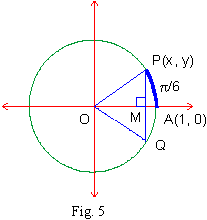
|