|
EXAMPLE 1
Find the fundamental period of f (t) = sin kt1 For k > 0
Solution : We know that,
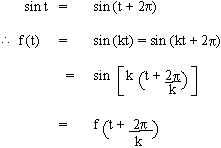
\ f (t) is periodic function with fundamental period
EXAMPLE 2
Find whether f (t) = cos (5t + 4) is periodic? If so, find its fundamental period.
Solution : Since cos t = cos (t +
2p)
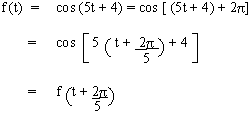
\ f (t) is a periodic function and the fundamental period is
2p/5.
EXAMPLE 3
Find a tangent function whose fundamental period is 9.
Solution: tan t = tan (t + p)
Let f (t) = tan kt be the required function
\ f (t) = tan kt = tan (kt + p)
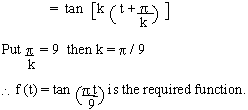
EXAMPLE 4
If sin x = 3/5 then what is the value of each of the following sin (x +
6p), sin (x + 36000),
sin(x -10800).
Solution: sin (x + 6p) = sin (x + 2p),
sin (x + 36000) = sin (x + 10p) = sin (x +
2p) and
sin (x - 10800) = sin (x - 6p) = sin (x -
2p)
\ sin (x + 6p) = sin (x + 2p) = sin (x -
2p) = 3/5 since the function is periodic with period
2p.
|