|
ii) Now observe the following graphs of y = sin x, y = sin 2x and y = sin 3x
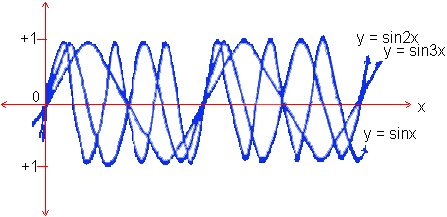 Click here to enlarge
Fig. 19
The next factor b in y = sin bx allows for period
variation (cycle length) of the sine function.
The period of the function y = sin bx is 2p / b. Note that b = | b |. Thus y = sin 3x has a
period of 2p / 3, y = sin 7x has period 2p / 7 etc. (This is also true for cosine function).
iii) The next additional factor is c in y = sin (x + c) allows a phase shift
(sliding of the graph to left or right) in the graph of sine function.
The phase shift is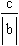 . It is always positive irrespective of c is positive
(shifting to the left) or negative (shifting the right). Also note that
sin x = cos (x - p/2) or cos x = sin (x + p/2). The discussion is also
true for cosine function. Cosine graph also has same appearance, except
the period shift of p/2 units to the left. . It is always positive irrespective of c is positive
(shifting to the left) or negative (shifting the right). Also note that
sin x = cos (x - p/2) or cos x = sin (x + p/2). The discussion is also
true for cosine function. Cosine graph also has same appearance, except
the period shift of p/2 units to the left.
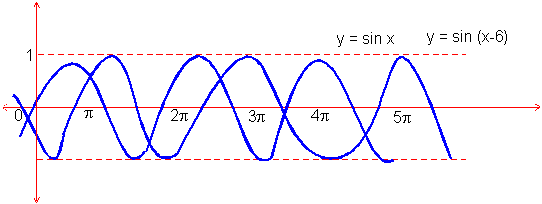 Click here to enlarge Click here to enlarge
Fig. 20
iv) Now we will see one more factor 'd' in function y = d + sin x which forces the function
i.e. y = sin x to have a vertical shift (upwards or downwards) along y-axis. This can be clear from
the following graphs.
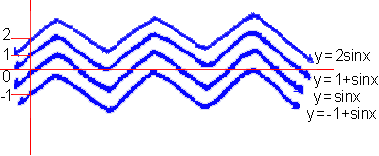
Fig. 21
Thus in a sine (or cosine) function of the form y = d + a sin (bx + c) or y = d + a cos (bx +
c) we have factors:
i) d ® For vertical shift (along y-axis)
ii) a ® For amplitude variation
(iii) b ® For period variation
(iv) c ® For phase shift.
|