|
5.4 Locally Increasing or Decreasing Functions
(I) Definition of a function increasing
at a point :
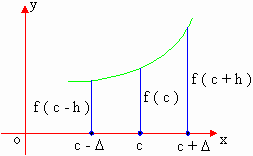
If there exists a number ,
such that f ( c - h ) < f ( c ) < f ( c ) + h ) for all h
satisfying 0 < h < D then
the function 'f' is said to increasing at x = c
(II) Definition of a function decreasing
at a point : -
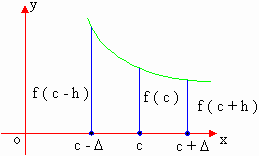
If there exists a number D
, such that f ( c - h ) > f ( c ) > f ( c + h ) for all h
satisfying 0 < h < D then
the function ’ f ’ is said to be decreasing at x =c
The careful study of these definitions, clearly states
that the function y = f ( x ) is increasing at x = c if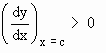 
i.e. f ' ( c ) > 0 and y = f ( x ) is decreasing at x = c if 
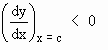i.e. f ' ( c ) < 0. Thus if a function is increasing at a point,
then the derivative is positive at that point and if a function is
decreasing at a point, then the derivative is negative at that point.
Also it is clear that a function f (x) is increasing in an interval
(a, b) if f ' (x)> 0, at every x Î
(a, b). Similarly a function f (x) is decreasing in an interval (a,
b) if f ' (x) < 0, at every x Î
(a, b).
[next page]
|
Index
5.1
Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions
5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And
Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation
Chapter
6
|
