|
5.10 Second Derivative Test For Local Extrema
Maximum points
Consider the point P (Fig 1). The gradient at P is zero for the curve y = f(x). The gradient is positive for all points to the immediate left of P and negative for all points to the immediate right of P.
Thus near P 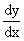 is changing its sign from positive, through zero to negative values, therefore at P, is changing its sign from positive, through zero to negative values, therefore at P, 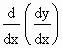 i.e. i.e. 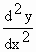 is negative. is negative.
Therefore, for maximum point,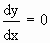 and and 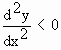
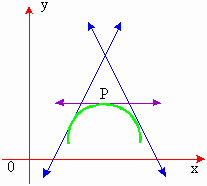
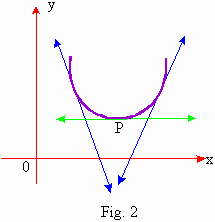
Minimum points
Consider the point P. The gradient there is zero.
For all points to the immediate right of P, the gradient
is positive while for all points to the immediate left of P, the gradient is negative. Thus near P, 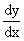 changes from negative, through zero to positive values. changes from negative, through zero to positive values.
Therefore, at 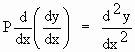 is positive. is positive.
Therefore,for a minimum point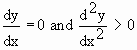
[next page]
|