Angle between two curves is the angle between two tangents lines drawn to the two curves at their point of intersection. If m₁ and m₂ are two slopes of these two tangents and q is the acute angle between them then we have tan q =

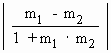
Let C₁ and C₂ be two curves intersecting at a point P. Then these curves are said to intersect 'orthogonally' at P. If tangents at P to C₁ and C₂ are at right angles i.e. m₁ m₂ = -1

Let the tangent and normal at 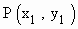to the curve y = f (x) meet x - axis at T and G respectively and Let PN be perpendicular to the x - axis at N. Then

(1) PT is called the "tangent length" at P
(2) PG is called the "normal length" at P
(3) The segment TN is known as the "sub-tangent" at P and
(4) The segment NG is known as the "sub-normal" at P

Then we have

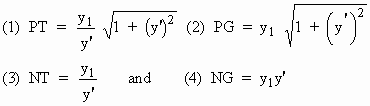
[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6