|
5.15 Differentials : Approximation and Errors
Recall the definition of the derivative of a function y = f (x)
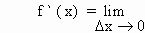 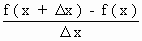
This represents the slope of tangent to the curve y = f (x) at some point (x,
f (x))
Now if Dx is very small (Dx ¹ 0), then the slope of tangent is approximately the same as the slope of the secant through (x, f (x))
i.e. 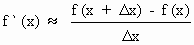
\ 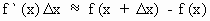
Now the differential of the independent variable x is written as dx and it is the same as Dx
\ dx = Dx
, Dx ¹ 0
Hence, f ‘ (x) . dx » f (x + Dx) - f (x) ... (1)
Similarly dy = Dy for the variable y, Dy ¹ 0.
we also have that Dy = f (x + Dx) - f (x)
\ dy = f (x + Dx) - f(x) ...(2)
Therefore from relations (1) and (2) we have dy = f ‘ (x) dx = Dy
Thus, when the change in x (Dx = dx) is relatively very small, then the differential of y (dy) is approximately equal to the exact change in y (Dy) i.e. The smaller the change in x, the closer dy to Dy. This fact enables us to approximate the functional value close to f (x)
Example 47
Find dy if y = x2 + 7x + 2
Solution : Let y = f (x) = x2 + 7x + 2
\ f ‘ (x) = 2x + 7
then dy = f ‘ (x) dx
\ dy = ( 2x + 7 ) dx
Example 48
Find dy if y = cos x + sin 2x
Solution : Let y = f (x) = cos x + sin 2x
then dy = f ‘ (x) dx
i.e. dy = ( 2 cos 2x - sin x ) dx
Approximations
Example 49
Find correct to 4 decimal places, the approximate
value of 2x3 + 7x + 1 at x = 2.001
Solution : Let f (x) = 2x3 + 7x + 1 then f ‘ (x) = 6x2 + 7
Then convenient value of x for f (x) is x =
2 which is relatively close to 2.001. \ f ‘ (2)
= 31
Also, x increases from x = 2 to x = 2.001
then we have Dx = 0.001
Now dy = f ` (x) . dx
\ dy = 31 . (0.001)
Now f (2) = 31
\ The approximate value of f (x) = 31 + 0.031 = 31.031
[next page]
|