|
5. 8 The Mean-value Theorem
For the theoretical purpose, the mean-value theorem is one of the most useful tools. The special and easy case of mean value theorem is the ‘Rolle's’ theorem, which will serve as a lemma for our main results.
Rolle’s Theorem : If ‘f’ is continuous on
[a, b] and differentiable in (a, b) and if, further f (b) = f (a),
then their exists at least one point x = c in (a, b) such that f
'(c ) = 0
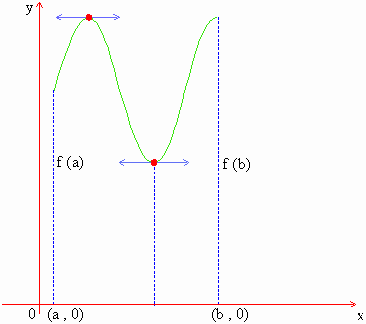
In this theorem, y = f (x) is continuous on [a, b] and differentiable in (a, b). Also f (b) = f (a). Hence the curve y = f (x) can be drawn as in the adjoining figure. The result f ‘ ( c ) = 0 means the tangent at x = c is parallel to x - axis. Hence y = f (x) is continuous on [a,b], differentiable in (a, b) and f (b) = f (a), then there exists at least one point on this curve at which the tangent is parallel to x - axis.
[next page]
|