|
5.13 Rate Measure (Distance, Velocity and Acceleration)
If y = s (t) represents the position function, then y = sí (t) represents the instantaneous
velocity i.e. 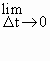
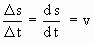 and a = ví(t) = s" (t) represents the
and a = ví(t) = s" (t) represents the
instantaneous acceleration at time t i.e. a = 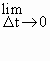 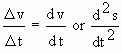
Note that a =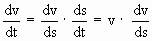
(1) If v > 0 (i.e. positive velocity) indicates that the position is increasing with increasing time while v < 0 (i.e. negative velocity) indicates the decreasing position as time decreases.
(2) If v = 0 implies that distance ísí remains constant on the given interval of time.
(3) If a > 0 implies that velocity is increasing with respect to time and a < 0 implies that the velocity is decreasing with respect to time.
(4) If v = constant on an interval of time, then a = 0 on that interval.
Example 36 A particle is moving in a straight line so that after ítí seconds its distance ísí from a fixed point O on the line is given by s (t) = 8t + t3.
Find (i) the velocity at time t and also t = 2
(ii) the initial velocity
(iii) acceleration at ítí and also at t = 2
Solution : s (t) = 8t + t3
(i) v = 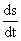 = 8
+ 3t2 = 8
+ 3t2
\ velocity
at (t = 2) = 8 + 12 = 20 unit /s
(ii) Putting t = 0, initial velocity = 8 + 3 ī 0 = 8 unit /s
(iii) Acceleration
a = 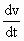 = 6t = 6t
\ acceleration
(at t = 2) = 6 ī 2
= 12 unit /s2
Example 37 The
position of a particle on a line is a given by s (t) = 2t3 - 9t2 + 12t .
Calculate its acceleration when it stops.
Solution : s (t) = 2t3 - 9t2 + 12t
\
v = 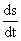 =
6t2 - 18t + 12 and a = =
6t2 - 18t + 12 and a = 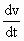 = 12t - 18
= 12t - 18
When the particle stops, its velocity (v) = 0
\ 6 (t2 - 3t + 2) = 0 Þ (t - 2) (t - 1) = 0
\ t = 1 and 2
When t = 1 a = 12 (1) - 18 = - 6 unit /s2 and
When t = 2
a = 12 (2) - 2 = 6 unit /s2
Example 38 A point moves
in accordance with the law v (t) = a + bt + ct2 and the initial velocity and
acceleration are 3 and 2 respectively. Also the acceleration at the end of 1st
second is 12. Find the velocity at the end of 3 seconds and the acceleration
at the end of 4 seconds.

[next page]
|