|
5.12 Concavity and Points of Inflection
The second derivative of a function may be also be used to determine the general shape of y = f (x) on a selected interval.
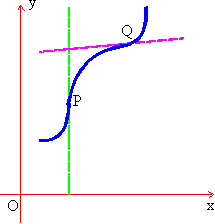
A point of inflection on a curve is a point where the curve changes its direction of curvature. See the adjoining fig. You will notice that at P the curve changes from being concave upward to being concave downwards. At Q, it changes from concave downwards to being concave upwards. Since f " (x) i.e. 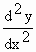 is the rate of change of the gradient is the rate of change of the gradient 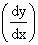 , a graph is concave upwards where f " (x) > 0 and concave downwards where f " (x) < 0. , a graph is concave upwards where f " (x) > 0 and concave downwards where f " (x) < 0.
Now at a point of inflection, the gradient stops increasing and begins decreasing, or it stops decreasing and begins increasing. Thus a point of inflection is one at which 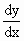 is either a maximum or a minimum. Thus the condition for a point of inflection is that is either a maximum or a minimum. Thus the condition for a point of inflection is that 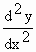 = 0 at the point and it changes sign in passing through it i.e. = 0 at the point and it changes sign in passing through it i.e. 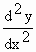 = 0 and = 0 and 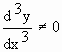 Note that , the tangent to a curve at a point of inflection crosses the curve, or more accurately, it cuts the curve at three coincident points. Note that , the tangent to a curve at a point of inflection crosses the curve, or more accurately, it cuts the curve at three coincident points.
Problems On Maxima And Minima With Concavity Of A Curve
Example 23
Determine the concavity of y = 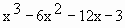 and identify any point of inflection.
and identify any point of inflection.
Solution : Since f (x) is a polynomial
in x, x  R
R
Now f ' (x) = 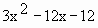
and f " (x) = 6x - 12
f "(x) = 0
Þ 6x
- 12 = 0
\ 6x = 12
\ x = 2
We find that f " (x) < 0 on ( -
•, 2) ®
Left of x = 2
and f " (x) > 0 on (2, •
) ® Right of x = 2
Hence f(x) is concave downwards on (- •,
2) and concave upwards on (2, •)
and f (x) has a point of inflection at (2, - 38)
[next page]
|