Example 16

If a, b, are real numbers, show that there exists at least one real number c

such that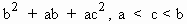

Solution : Let f (x) = x³ over [a, b]

f (x) is continuous on [a, b] and differentiable in (a, b). Also f (b) = b³ and f ' (x) = 3x².

Since f (x) satisfies all the conditions of mean-value theorem, there exists

at least one x=c, a < c < b such that

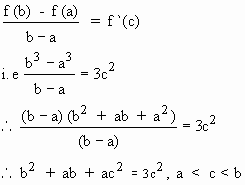
Example 17

Using mean - value theorem, prove that

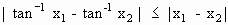
Solution : Let f (x) = tan^-1x over [x₂, x₁]

Now f (x) is continuous on [x₂ , x₁] and differentiable in (x₂,x₁)

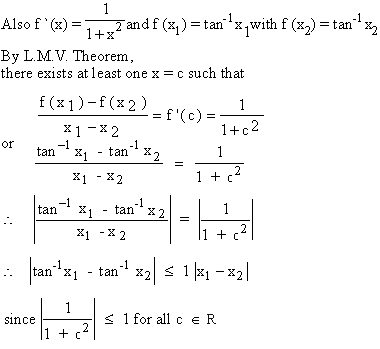
[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6