|
Technique
(1) Find f '(x) and f " (x).
(2) Find the roots (i.e. critical points) of f ' (x) = 0.
Let x = a, x = b, x = c etc be these critical points of f (x).
(3) If f " (a) < 0, then f (x) has a local maximum at x = a and if f " (a) > 0,
then f (x) has a local minimum at x = a. But if f " (a) = 0. Then the test fails.
(4) Use the same procedure for all critical points of f (x) as it has been given in (3).
Drawbacks :
(I) 1) f ' (x) = 0 and f" (x) = 0
2) f ' (x) = 0 and f "(x) DNE
3) f ' (x) DNE
Under any of these conditions, the first derivative test would have to be used instead the second derivative test.
(II) In case of some functions, the second derivatives are very difficult and tedious to calculate. Thus relent back to the first derivative test to find the Local extrema.
Example 20
Find the relative maxima and minima of f (x) =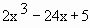 
Solution : f (x) =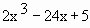 
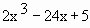
\ f ' (x) = 6x2
- 24 and f " (x) = 12 x
\ Critical
points are, f ' (x) = 0 Þ or
i.e. x = 2 and x = - 2
Since f " (- 2) = 12 (- 2) = - 24 < 0.
' f ' has relative maxima at x = - 2.
Thus f ( - 2) = 2 (-2)3 - 24 (-2) + 5 = 37
The relative maximum value of f (x).
Also, f " (2) = 12 (2) = 24 > 0.
Therefore 'f ' has a relative minima at x = 2 and
f (2) = 2 (2) 3 - 24 (2) + 5 = -27 the relative minimum value of f(x).
Example 21
Examine f (x) =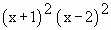 
for the relative maximum and minimum values.
Solution :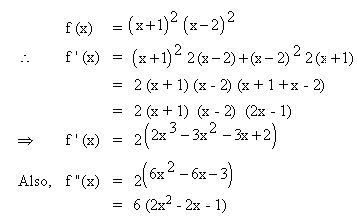 
[next page]
|
