|
Example 28
A page is to contain 54 sq.cms of printed material. If the margins
are 1cm at top and bottom and 0.5cm at sides, find the most economical
dimensions of the page.
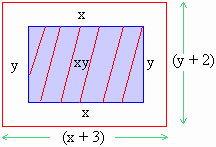
Solution : Let the dimension of the printed
material be x cm. and y cm.
Then xy = 54 \ y = 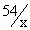
The dimension of the page are
(x + 3) and (y + 2) cm. Then the area
of the page is A = (x + 3) (y + 2)
\ A = (x + 3) 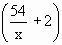
= 60 + 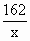 + 2x + 2x
Then = 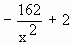 and critical points are x = + 9 and critical points are x = + 9
Also, 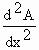 = = 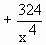
\ 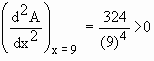
\ The relative minimum is
at x = 9
\ The
required dimensions of the page are (x + 3) = 12 cm and y = 54 /9
= 6 Þ (y + 2) = 6 + 2 =
8 cm i.e. 12 cm wide and 8 cm high.
Example 29
A box with a square base is to have an open top. The area of the
material for making the box is 192 sq. cm. What should be its dimensions
in order that the volume is as large as possible?
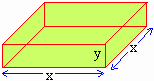
Solution : Let the dimensions of the base of the open
box be x cm and x cm and height be y cm.
\The area of the material of the open box = (area of the
base) + 4 (area of vertical face)
\
192 = (x ´ x) + 4 (xy)
\
192 = x2 + 4xy
\
y = 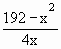
[next page]
|