|
Example 41 The side of a cube are increasing at the rate of 0.5 cm/sec. At what rate its surface area and volume is increasing when the side is 10 cm long?
Solution : 1) The surface area (s) of a cube of side x is s = 6x2
By Differentiating w. r. to ’ t ’ , we get
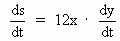
where  =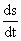
rate of change of surface area
and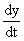
= rate of change of the side of the cube.
Given that when x = 10 cm.
=
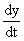0.5 cm /sec, then
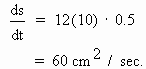
2) The volume (v) is given by v = x3
\ 
\ 
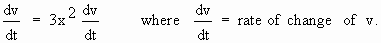
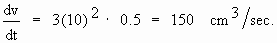
Example 42 The top of a ladder 20 units long is resting against a vertical wall and its foot on a level pavement, when the ladder beings to slide. When the foot of the ladder is 12 units from the wall, it is sliding away from the wall at the rate of 2 units / sec find the rate at which the top is sliding down.
Solution :
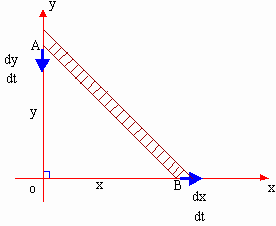
Let AB = 20 units be the length of the ladder.
We have in right angled triangle AOB,
AB2 = AO2 +OB2
\ (20)2 = y2 + x2
i.e. x2 + y2 = 256
Also given that OB = x = 12 units
\ (12)2 + y2 = 400
\ y2 = 256
\ y = 16 units
Now differentiating w. r. to ’ t ’ , x2 + y2 = 400 we get
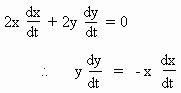
Also.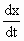
= 2 units / sec = rate of sliding away from the wall.
\ 16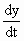
= - 12(2)
\ 
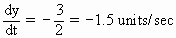
\ The rate which the top is sliding down = 1.5 units/sec
[next page]
|
