|
Example 53
The radius of a sphere is measured as 24 cm with
an error of 0.01cm. Find (I) the approximate error (II) relative
error and (III) percentage error in calculating its volume.
Solution : If
r is the radius of the sphere, then its volume is 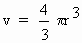
\ 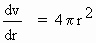
\
approximate error in volume (dv) = 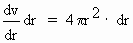
\ when
r = 24 and dr = 0.01 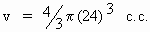
Relative error = 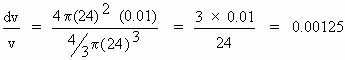
Percentage error = 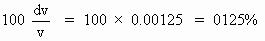
Example 54
The time T of a complete
oscillation of a simple pendulum of length l is given
by 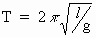 , where g is a constant. If there is an error of 2% in the value
of l , find the
, where g is a constant. If there is an error of 2% in the value
of l , find the
approximate error and percentage error in the calculated
value of T.
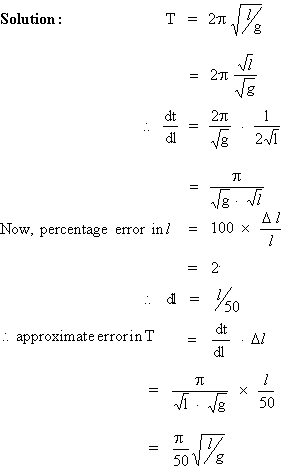
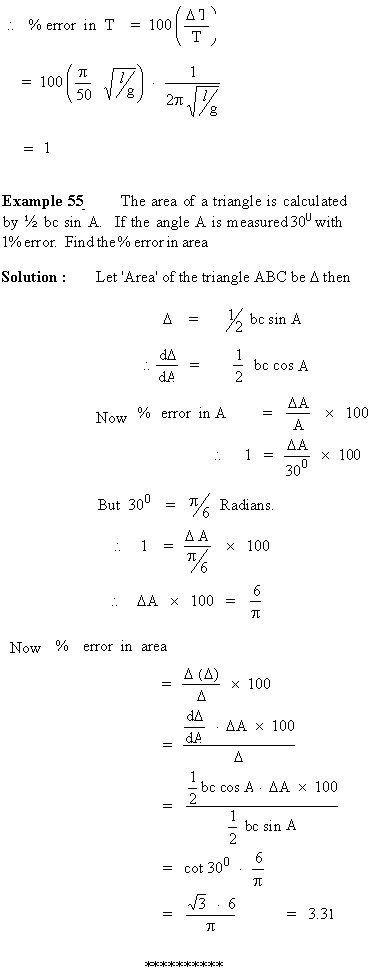
[next chapter]
|