Example 11

Find the critical points of f (x) = 2x⁴ - 32x2

Solution : Since f (x) is a polynomial in x, x Î R.

Now f ' (x) = 8x³ - 64x

\ For critical points, f ' (x) = 0 Þ 8x³ - 64x = 0

8x (x² - 8) = 0

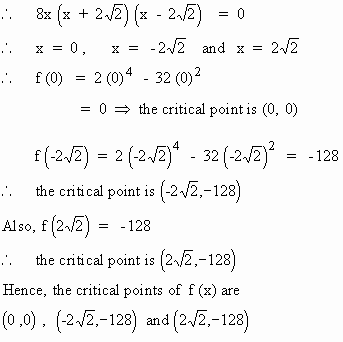
Example 12

Find all critical points of f (x) = sin x + cos x on [0 , 2 p]

Solution : Given that for f (x) = sin x + cos x , x Î [0, 2 p]

Now f ' ( x ) = cos x - sin x

for critical points, f ' ( x ) = 0 Þ cos x - sin x = 0

\ cos x = sin x Þ tan x = p/4

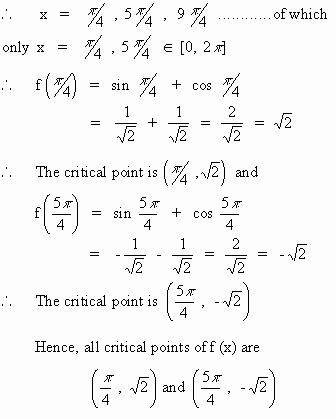
[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6