Example 14

Verify that f (x) = e^x sin x satisfies the hypothesis for the Rolle’s theorem on [0, p] and find number c described in the theorem.

Solution : f (x) = ex sin x is continuous on [0, p] and differentiable in (0, p)

Also, f (0) = f (p) = 0

\ All the conditions of the Rolle’s theorem are satisfied.

\ There exists a x = c Î(0, p) such that f ' (c) = 0

Now f '(x) = e^x cos x + e^x sin x

= e^x (cos x + sin x)

\ f '(c) = e^c (sin c + cos c)

\ 0 = e^c (sin c + cos c)

OR sin c + cos c = 0 Þ tan c = -1 Þ c = 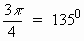Î(0, p).

Hence the Rolle's theorem is verified.

Example 15

Verify Mean-value theorem for x - x³ in (-2 , 1)

Solution : f (x) = x - x³

\ f '(x) = 1 - 3x²

\ f (x) is continuous on [ -2, 1] and derivable in (-2, 1) and

f (-2) = -2 + 8 = 6 and f (1) = 1 - 1 = 0

All conditions of L.M.V. theorem are satisfied.

\ There exists one x = c in (-2 , 1) such that

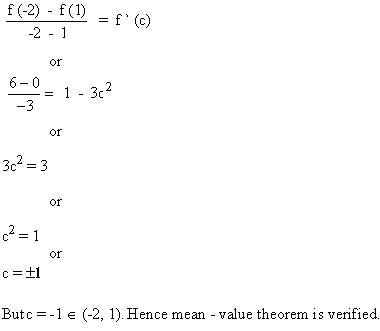
[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6