Example 24

Determine the concavity of f (x) = cos x + sin x on [0, 2p] and identify any points of inflection.

Solution : f (x) = cos x + sin x and x Î [0, 2p]

Also, f ’ (x) = cos x - sin x and

f " (x) = - sin x - cos x

Now f " (x) = 0

Þ - sin x = cos x

\ tan x = -1

\ x = 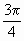, 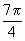Î [0, 2p]

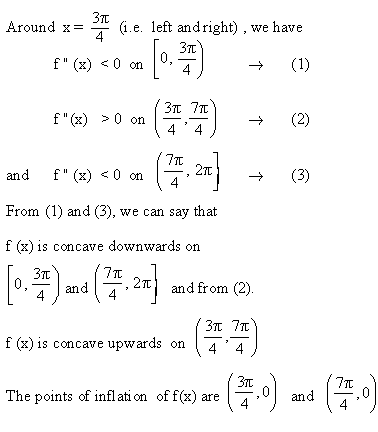
[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6