|
Example 25
The perimeter of a rectangle is 100 cm. Find the dimensions
of the rectangle when its area is maximum.
Solution : Let the length of the rectangle be 'x' cm
and breadth be 'y' cm.
Let its area be A sq. cm.
Now given that perimeter = 100 cm
\ 2 ( x + y) = 100
\ x + y = 50
\ y = 50 - x
Then A= xy = x (50 - x)
By Differentiating w.r.to x, we get
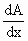 = 50 - 2x = 50 - 2x
and 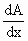 = 0 = 0
gives 50 - 2x = 0
i.e. x = 25 (critical point)
also, f "(x) = -2
Þ f "(25) = -2
< 0
By the second derivative test, A is maximum at x=25 Þ
y=25
\ when the area is maximum,
the rectangle is a square of side 25 cm.
Example 26
Divide 15 into two parts such that the product of the
square of one and the cube of other is maximum.
Solution : 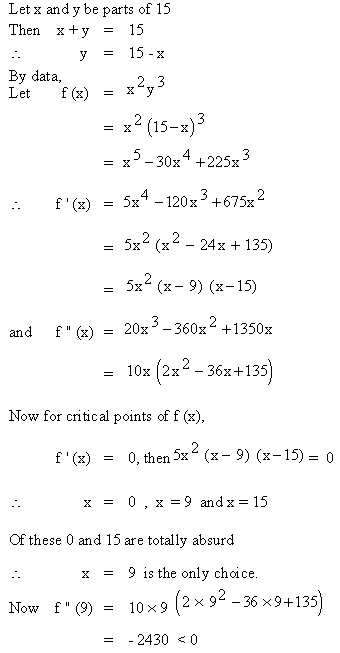
By the second derivative test ‘f’ has a relative maximum when x = 9
Also, when x = 9
then y = 15 - 9
= 6
\ The two required parts of
15 are 9 and 6.
[next page]
|