|
Example 27
Find the inflection points and plot the graph of the curve y =
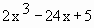 .
.
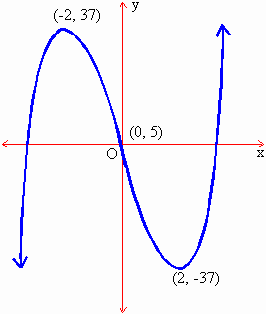
Locate its x and y intercepts if they can be found and the relative maximum and minimum points.
Solution : f (x) = 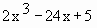
\ f ' (x) = 6x2
- 24
and f "(x) = 12x
with f "(x) = 12
Since f"(x)=12(0)
=0
and f" (0)=12 Ļ0
then (0, f (0)) i.e. (0, 5) is an
inflection point of f(x)
Put x = 0 in y = 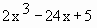
Þ y = 5 (the y intercept)
Notice that x intercept canít be determined (why ?)
Also f ' (x) = 0 Þ x2 = 4
i.e. x = + 2
(critical points of f (x).
Now f "(-2) = 12 (-2)
= - 24 < 0
\ ' f ' has a relative maximum
at x = -2
\ f (-2) = -27
\ (-2, 27) is a relative maximum
point and f " (2) = 24 > 0
(2, - 27) is a relative minimum point of f (x).
[next page]
|