|
4.8 Derivative of A Composite Function
Definition :
If f and g are two functions defined by y = f(u) and u = g(x) respectively then a function defined by y = f [g(x)] or fog(x) is called a composite function or a function of a function.
The theorem for finding the derivative of a composite function is known as the CHAIN RULE.
Theorem :
If f and g are differentiable and are defined by y = f (u) and
u = g (x), then the composite function y = f [ g (x) ] is differentiable
and we have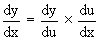 
Corollary :
If y = f (u), u = g (v) and v = h (x) where f, g and h
are differentiable functions of u, v and x respectively, then
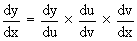
Example 18
Show that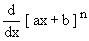 
= 
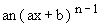
Solution :
Let y =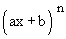 
and u = ax + b
\ 
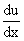= a
Then,
y = un
\ =
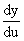nun-1
=
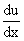n(ax + b) n-1
Now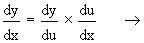 
by chain rule.
\ 
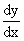= n(ax + b) n-1 x a
= an(ax + b) n-1
Example 19
Find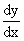
if y = (2x3 – 5x2 + 4)5
Solution :
Let y = u5
and u = 2x3 – 5x2 + 4
\=
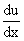6x2 – 10x
\ =
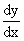5u4
Now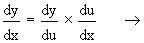
by chain rule.
\ 
|
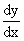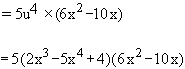
