1. f (x)  =  |x| + |x-1| " x ÎR is continuous at x = 0 but not derivable at x = 0

2. f (x)  =  0, if x £ 0
   

   = x, if x > 0 is continuous at x = 0 but not derivable at x = 0

3. f (x) = 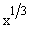is continuous over its entire domain of real numbers, but its derivative does not exist at x = 0.

4. f (x) = |x+2| is continuous over the entire domain of real numbers but is not derivable at x = -2

* THUS - Differentiability Þ continuity. But continuity does not imply differentiability.

Index

4. 1 Derivability At A Point
4. 2 Derivability In An Interval
4. 3 Derivability And Continuity Of A Function At A Point
4. 4 Some Counter Examples
4. 5 Interpretation Of Derivatives
4. 6 Theorems On Derivatives (differentiation Rules)
4. 7 Derivatives Of Standard Functions
4. 8 Derivative Of A Composite Function
4. 9 Differentiation Of Implicit Functions
4.10 Derivative Of An Inverse Function
4.11 Derivatives Of Inverse Trigonometric Functions
4.12 Derivatives Of Exponential & Logarithmic Functions
4.13 Logarithmic Differentiation
4.14 Derivatives Of Functions In Parametric Form
4.15 Higher order Derivatives

Chapter 5

Follow @Pinkmonkey_com