|
4.12 Derivatives of Exponential and Logarithmic Functions
The number ‘ e ’
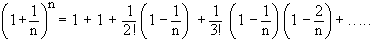
Therefore the limit of 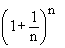 ,
as n approaches infinity is ,
as n approaches infinity is 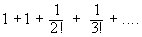
The number defined by 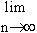 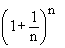 , or by the sum of the convergent series , or by the sum of the convergent series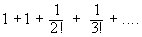 , is denoted by ‘ e ’. Its value, correct to 6 decimal places is 2 . 718282 i.e. clearly 2 < e < 3. It is also a fundamental constant like p and it is the
base of the natural or Napierian, or hyperbolic, logarithms. , is denoted by ‘ e ’. Its value, correct to 6 decimal places is 2 . 718282 i.e. clearly 2 < e < 3. It is also a fundamental constant like p and it is the
base of the natural or Napierian, or hyperbolic, logarithms.
The exponential function ex which is sometimes written as
e x p x is 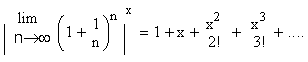
Another important function is 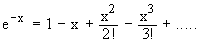
* Exponential functions in which a variable quantity occurs as
an index, or exponent.
The function 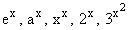 are examples of exponential functions. are examples of exponential functions.
Now , let y = f ( x ) = ex then f ( x + h ) = e x + h
= ex . eh
Then by the 1st principal of derivatives we get 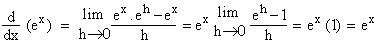
Differentiation of 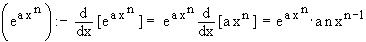
Differentiation of ‘log x’:-
Let y = logyex i.e. f ( x ) = log x Þ f ( x + h ) = log ( x + h )
|