If an equation is expressed as y = f(x), then y is said to be the explicit function of x. However if y is connected with x by an expression f (x, y) = 0, then y is said to an implicit function of x. For e.g. x² + 3xy + y² = 0.

For differentiating the implicit function we differentiate each term w.r.to x keeping in mind that if there is a term contains powers of y, we differentiate first w.r.to. y and then multiply it by 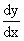to get its differentiation w.r.to x.

Index

4. 1 Derivability At A Point
4. 2 Derivability In An Interval
4. 3 Derivability And Continuity Of A Function At A Point
4. 4 Some Counter Examples
4. 5 Interpretation Of Derivatives
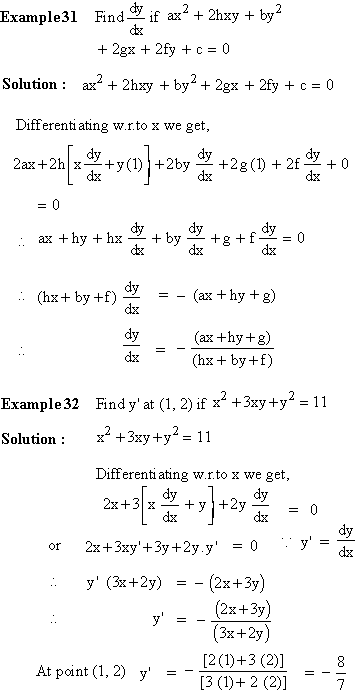
4. 6 Theorems On Derivatives (differentiation Rules)
4. 7 Derivatives Of Standard Functions
4. 8 Derivative Of A Composite Function
4. 9 Differentiation Of Implicit Functions
4.10 Derivative Of An Inverse Function
4.11 Derivatives Of Inverse Trigonometric Functions
4.12 Derivatives Of Exponential & Logarithmic Functions
4.13 Logarithmic Differentiation
4.14 Derivatives Of Functions In Parametric Form
4.15 Higher order Derivatives

Chapter 5

Follow @Pinkmonkey_com