|
4.5 Interpretation Of Derivative
1. The derivative of a function at a point is the slope of the tangent line at that point. It may be thought of the limiting position of the secant line to a curve y = f (x) at a point is the tangent at the point. Thus the limit of the slope of the secant line through a fixed point on the curve and any other points on the curve that get closer and closer to the fixed point when this limit exists. It is the slope of the tangent line at that fixed point (x, f (x)) on the curve y = f (x).
2. The derivative is the instantaneous velocity of a function representing the position of a particle along a line at time ‘t’ where y = f (x). The derivative may be thought of as the limit of the average velocities between a fixed time and other times that get near and nearer to this fixed time. When this limit exists, the instantaneous velocity at time t for y = f (t).
3. The derivative is the instantaneous rate of change of a function at a point. It may be thought of as the limit of the average rates of change between a fixed point and other point on the curve that get closer and closer to that fixed point. When this limits exists, it is known as the instantaneous rate of change of the function y = f (x) at the fixed point (x, f (x) ).
Note : When you are asked to
find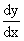 
if y = f (x); by first principle of derivatives, use the definition.
i.e.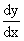
=  
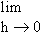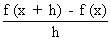if it exists.
Example 5
Find the instantaneous velocity of s (t) =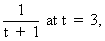 
using first principle of derivative.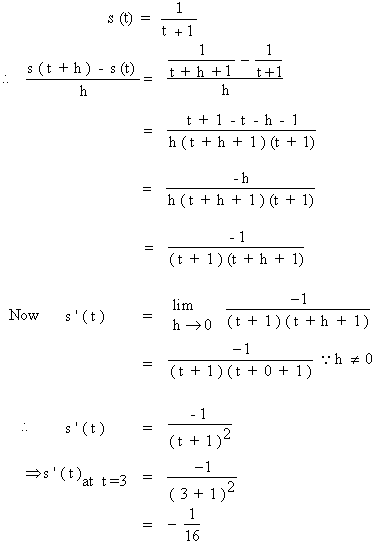 
The negative sign indicates that the particle is moving in the negative direction.
|
