If y = f ( x ) then y' = f' ( x ). This derivative is itself a function. Consider the derivative of f' ( x ) which is denoted by f' ( x ). This is known as second order derivative. This can be continued to third, fourth and so on. Thus you can have successive derivatives of f ( x ), which are known as the higher order derivatives of f (x). Instead of using the "prime" notation which is messy, it is advisable to use a numerical notation like

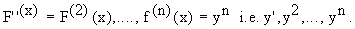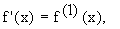
This process is known as the successive differentiation.

Example 72 Find

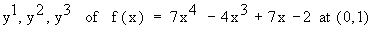
Solution :         y = f ( x )

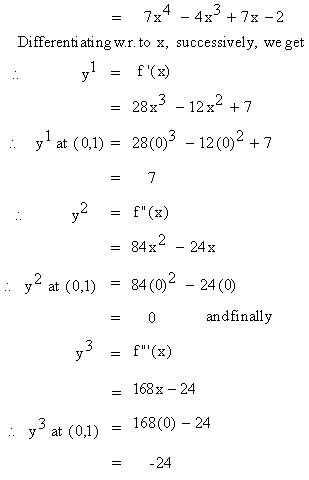
Index

4. 1 Derivability At A Point
4. 2 Derivability In An Interval
4. 3 Derivability And Continuity Of A Function At A Point
4. 4 Some Counter Examples
4. 5 Interpretation Of Derivatives
4. 6 Theorems On Derivatives (differentiation Rules)
4. 7 Derivatives Of Standard Functions
4. 8 Derivative Of A Composite Function
4. 9 Differentiation Of Implicit Functions
4.10 Derivative Of An Inverse Function
4.11 Derivatives Of Inverse Trigonometric Functions
4.12 Derivatives Of Exponential & Logarithmic Functions
4.13 Logarithmic Differentiation
4.14 Derivatives Of Functions In Parametric Form
4.15 Higher order Derivatives

Chapter 5

Follow @Pinkmonkey_com