|
4.2 Derivability in an Interval
A function ‘f’ defined on [a, b] is derivable at the end point a
i.e. f ’ (a) exists if
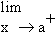 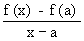 exists exists
Similarly it is defined at the end point b, if
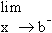 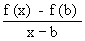 if
exists. if
exists.
If a function is derivable at all points of an
interval except the end points a and b, it is said to be derivable in an
open interval (a, b).
A function is derivable in the closed
interval [a, b] if it is derivable in the open interval (a, b) and
also at the end points a and b.
Example 2 Show that the function f (x)
= x2 is derivable on [0, 1]
Let x0 be any point of (0, 1), then
f ’ (x 0 ) = 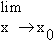 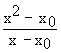
= 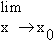 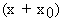
= 2x0
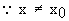
At the end points, we have
f ’ (0) = 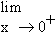 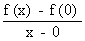
= 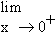 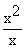
= 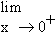 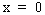
and
f ’ (1) = 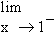 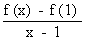
= 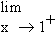 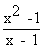
= 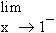 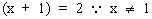
Thus the function is derivable in [0, 1].
|