|
4.10 Derivative of An Inverse Function
In algebra x-1 is also written as 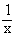 and it is the reciprocal of ‘x’. However in trigonometry, the -1 has a different meaning, and cos-1x stands for the angle whose cosine is ‘x’. Now ‘-1’ becomes the part of the symbol cos. Similarly sin-1x is the angle whose sine is ‘x’. However there are infinite number of angles which have same sine, cosine and tangent, etc. It is usual to consider only their principal values. Thus each of the six basic trigonometric functions have corresponding inverses when appropriate restrictions are placed on the domain of their original functions. All these inverse functions have derivatives. and it is the reciprocal of ‘x’. However in trigonometry, the -1 has a different meaning, and cos-1x stands for the angle whose cosine is ‘x’. Now ‘-1’ becomes the part of the symbol cos. Similarly sin-1x is the angle whose sine is ‘x’. However there are infinite number of angles which have same sine, cosine and tangent, etc. It is usual to consider only their principal values. Thus each of the six basic trigonometric functions have corresponding inverses when appropriate restrictions are placed on the domain of their original functions. All these inverse functions have derivatives.
THEOREM : If y = f (x) is a derivable
function of x such that the inverse function x = f -1
(y) is defined then 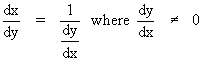
|