8.6 Central Limit Theorem
What we have discussed above with an example, is stated as a theorem called Central limit theorem. It states that 'when the size of the sample increases and becomes sufficiently large the distribution of the sample means tends to Normal Distribution'.
Now here we must take one thing in our notice that the theorem is equally valid for both normal and strongly non-normal. We restate the central limit theorem as: "Even if the population distribution is strongly non-normal, its sampling distribution of means tends to normal distribution for large sample size".
The natural question that comes to one’s mind is as to what will be the size which can be taken as the large size?
The following diagrams show how sampling distribution of means approaches normal distribution even if the parent distribution is not normal.
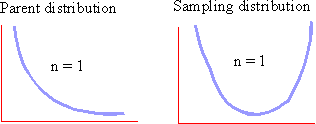
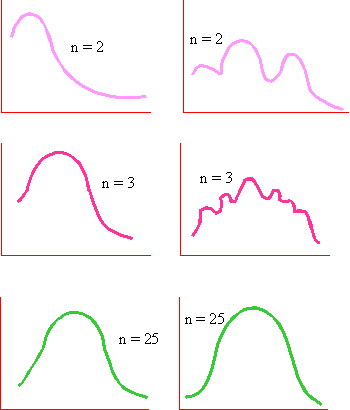
The answer to the above question is that the "large sample
size" means n > 30 i.e. over 30.
We have seen that the sample mean 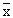 is distributed normally with mean m , the mean of the population
which is an unbiased estimator. It can be shown that the standard
deviation of the sample means, called Standard error (S.E.)
is equal to
is distributed normally with mean m , the mean of the population
which is an unbiased estimator. It can be shown that the standard
deviation of the sample means, called Standard error (S.E.)
is equal to 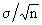
Thus 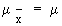 and and
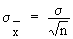
If we put, 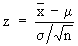 then z - score is called a standard normal variate, with the
mean as zero and the standard deviation as 1. If m is the population mean and then z - score is called a standard normal variate, with the
mean as zero and the standard deviation as 1. If m is the population mean and 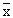 is the sample mean then is the sample mean then 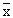 - m is the deviation of the sample mean from the population mean. - m is the deviation of the sample mean from the population mean.
When this deviation is divided by 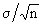 , the ratio , the ratio 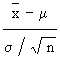 is called the relative deviation of the sample mean from the population mean. is called the relative deviation of the sample mean from the population mean.
|