|
8.20 Testing difference between Means of two samples Dependent samples or Matched paired observations
Two samples are said to be dependent on each other when the elements of one are related to those of the other in any significant or meaningful manner. In fact the two samples consists of observations made of the same objects, individuals or more generally, on the same selected population elements. The ' t ' test is often used to compare ' before ' and ' after ' scores in experiments for the determination of the significant change that has occurred. We may carry out some experiment, say, to find the training effect on some students, to find out the efficacy of coaching class, efficacy of two drugs. Often the use of dependent or paired samples will enable us to perform a more precise analysis.
The ' t ' test is defined by the formula :
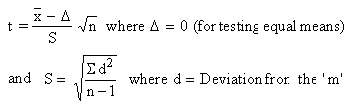
where m = mean of the differences.
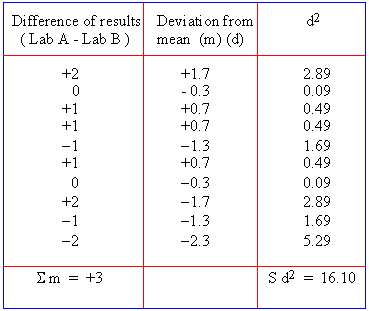
Example Two laboratories carry out independent
estimates of fat content in the ice-cream of a certain company.
A sample is taken from each batch, halved and the separate halves
were tested in the two laboratories. They obtain the following results
:
% of fat content in ice-cream
Batch No. 1 2 3 4 5 6 7 8 9 10
Lab A 7 8 7 3 8 6 90 4 7 8
Lab B 9 8 8 4 7 7 9 6 6 6
Is the testing reliable ?
Solution: The null hypothesis Ho
: m1
- m2
or Ho : m1
- m2
= 0
i.e. If the testing is reliable the mean of the difference in the results should not be significantly differ from 0.
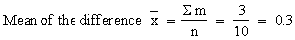
|