|
8.21 Chi-Square
Tests like z-score, t, F are based on the assumption that the samples were drawn from normally distributed populations or more accurately that the sample means were normally distributed. As these tests require assumption about the type of population or parameters, these tests are known as 'parametric tests.'
There are many situations in which it is impossible
to make any rigid assumption about the distribution of the population
from which samples are drawn. This limitation led to search for
non-parametric tests. Chi-square (Read as Ki - square) test of independence
and goodness of fit is a prominent example of a non-parametric test.
The chi-square ( c2
) test can be used to evaluate a relationship between two nominal
or ordinal variables.
c2
(chi-square) is measure of actual divergence of the observed and
expected frequencies. In sampling studies we never expect that there
will be a perfect coincidence between actual and observed frequencies
and the question that we have to tackle is about the degree to which
the difference between actual and observed frequencies can be ignored
as arising due to fluctuations of sampling. if ;there is no difference
between actual and observed frequencies then c2
= 0. If there is a difference, then c2
would be more than 0. But the
difference may also be due to sample fluctuation and thus the value
of c2
should be ignored in drawing the inference. Such values of c2
under different conditions are given in the form of tables and if
the actual value is greater than the table value, it indicates that
the difference is not solely due to sample fluctuation and that
there is some other reason.
On the other hand, if the calculated c2
is less than the table value, it indicates that the difference may
have arisen due to chance fluctuations and can be ignored. Thus
c2-test
enable us to find out the divergence between theory and fact or
between expected and actual frequencies is significant or not.
If the calculated value of c2
is very small, compared to table value then expected frequencies
are very little and the fit is good.
If the calculated value of c2
is very large as compared to table value then divergence between
the expected and the observed frequencies is very big and the fit
is poor.
We know that the degree of freedom r (df) is the number of independent constraints in a set of data.
Suppose there is a 2 ´
2 association table and actual frequencies of the various classes
are as follows :
| |
A |
a |
|
| B | AB | aB | 60 |
| |
-22 |
-38 |
|
| | | | |
| b |
Ab |
ab |
40 |
| | -8 | -32 | |
| |
|
|
|
| | 30 | 70 | 100 |
Now the formula for calculating expected frequency
of any class ( cell )

For example, if we have two attributes A and B that are independent then the expected frequency
of the class (cell) AB would be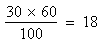
Once the expected frequency of cell (AB) is decided the expected frequencies of remaining three classes are automatically fixed.
Thus for class (aB) it would be 60 - 18 = 42
for class (Ab) it would be 30 - 18 = 12
for class (ab) it would be 70 -
42 = 28
This means that so far as 2 ´
2 association ( contingency ). Table is concerned, there is 1 degree
of freedom.
In such tables the degrees of freedom are given by a formula n = (c - 1) (r - 1)
where c = Number of columns
r = Number of rows
|