|
8.23 Sampling Theory of Regression
The regression equation of a normally distributed population is y = a + bx.
Let the regression equation of a sample drawn from it be
y = a + dx.
All you have done is, replaced the intercept ( a ) by c and the slope ( b ) by d.
To find S. E. of regression coefficient of y on x i.e. S. Ebyx use 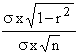
To find S. E. of regressiojn coefficient of x on y i.e. S.Ebxy use 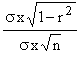
Also S. E. of regression estimate of y on x or S. Exy = 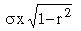
S. E. of regression estimate of x on y or S. Eyx =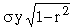
To test b = c use t =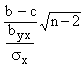 width df = n-2 width df = n-2
This can be used to find confidence intervals for population regression coefficient from sample values.
Example Find the regression coefficient
of the prices of city A over the prices of city B given that :
A B
Average price per kg 120 130
Standard deviation 4 5
Coefficient of correlation 0.6
n = 100
Solution: Now regression coefficient
of prices of city A (x) over the prices of city B.
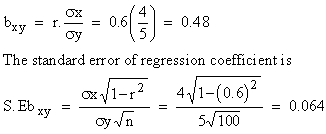
Thus the regression coefficient of prices of the city A over the prices of city B is 0.48 and its S.E. is 0.064.
Example For a certain group of adults,
the coefficient of correlation between height and weight is 0.7.
Standard deviations of height and weights are 2 inches and 10 lb
respectively and the means of heights and weights for the entire
group are 70 inches and 130 lbs respectively. Find out the best
estimate of weight of a member who is 65 inches tall. Assign limits
to this estimate, within which all probability has actual weight
would lie.
Solution: Weight (y) and height (x)
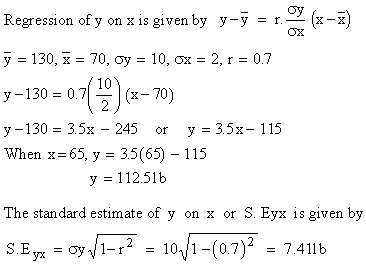
Thus the best estimate of weight of an member whose weight is 112.5 lb and
height 65 inches cannot deviate from the actual weight by more than 3 S. E.
\
The estimate of all probabilities of his weight lies between
= 112.5
± 3 ( 7.41 )
= (
112.5 - 22.23, 112.5 +
22.23 )
= ( 90. 27 lb, 134.73 lb )
**********
|