8.14 Testing The Difference Between Means
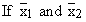 denote the means of the samples drawn from the first and second population respectively, having means m1 and m2 and standard deviations s1 and s2 and if the sizes of the samples are n1 and n2, then it can be proved that the distribution of the difference between the means denote the means of the samples drawn from the first and second population respectively, having means m1 and m2 and standard deviations s1 and s2 and if the sizes of the samples are n1 and n2, then it can be proved that the distribution of the difference between the means 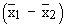 is normal with mean (m1 - m2 ) and S.D. is given by is normal with mean (m1 - m2 ) and S.D. is given by
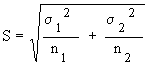
Therefore,
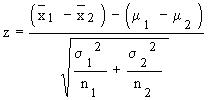
Further, under the hypothesis Ho : m1 = m2 or Ho : m1 - m2 = 0 We see that
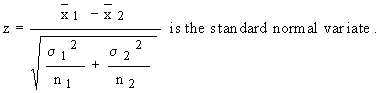
When the two samples belong to the same population, we have s1 = s2 = s then,
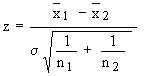
Similarly, the confidence limits for ( m1 - m2 ) at various levels of confidence are :
1)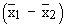 ± 1.96 S at 95% level of confidence ± 1.96 S at 95% level of confidence
2)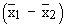 ± 2.58 S at 99% level of confidence ± 2.58 S at 99% level of confidence
3)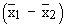 ± 3. S at 99.73% level of confidence. ± 3. S at 99.73% level of confidence.
1. Note: Here S = S.E. = 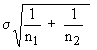
For the samples drawn from the same population.
2. Note: If S.D. of two populations
i.e. s1 , s2
are unknown, we use s.d. of samples in their places.
|