8.11 Sampling Of Variables
The sample mean 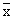 is normally distributed with mean m and standard deviation s /Ön where m is the mean of the population and s is the standard deviation of the population. This results will help us in testing a hypothesis about the population mean.
1. Testing the hypothesis that the population mean m = m0 which is a specified
value.
Now s = S.D. of the population is known.
In notations :-
The null hypothesis : m = m0 i.e. m - m0 = 0. First calculate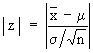 
If | z | < 1.96, the difference is not significant at 5% level and Ho is accepted, otherwise rejected. If | z | < 2.58, the difference is not significant at 1% level and Ho is accepted, otherwise rejected.
Note: We have assumed that s
is known. If however s is not known,
we take s to be equal to the S.D. of
the sample.
Example A random sample of 400 male students have average weight of 55 kg. Can we say that the sample comes from a population with mean 58 kg. with a variance of 9 kg. ?
Solution: The null hypothesis Ho
is that the sample comes from the given population.
In notations : Ho : m = 58 kg. and Ha : m ¹ 58 kg.
Now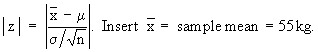 
m = population mean = 58 kg. n = 400 and s = population S.D. = 3
Therefore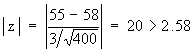 
This value is highly significant. We will reject Ho on the basis of this sample. The sample therefore, is not likely to be from the given population.
Example A random sample of 400 tins of vegetable
oil and labeled "5 kg. net weight" has a mean net weight of 4.98
kg. with standard deviation of 0.22 kg. Do we reject the hypothesis
of net weight of 5 kg. per tin on the basis of this sample at 1%
level of significance ?
Solution: The null hypothesis Ho
is that the net weight of each tin is 5 kg.
In notations Ho : m = 5 kg.
Inserting, 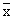 = 4.98 kg., m = 5 kg. s = 0.22 kg. and n = 400
In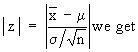
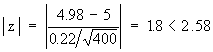
Hence Ho is accepted at 1% level of significance.
|
