8.16 Two tailed and One tailed Tests
While testing a hypothesis, we often talk of two-tailed tests and one-tailed tests. In the previous tests the critical region lay along both the tails of the distributions. That is, we did not want sample statistic ( say mean ) to be away from the population parameter (say mean) in either direction. The test for such a hypothesis is non-directional or two-sided or two-tailed. A two-tailed test of hypothesis will reject the null hypothesis Ho, if the sample statistic is significantly higher than or lower than the hypothesized population parameter. Thus in two-tailed test the rejection (critical) region is located in both the tails.
For example, suppose you suspect that a particular 6th grader’s performance on a test in Mathematics is not a true representative of the students who have appeared. The national mean score in this test was found to be 75. The alternative (or research) hypothesis is :
Ha : m ¹
75 while the null hypothesis is : Ho : m
= 75.
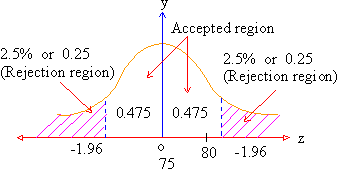
Now our pre-determined probability level is 95% i.e. 5% level of significance for this test. Both tests have the rejection (or critical) region of 5% i.e. 0.05. Now this rejection region is divided between both the tails of the distribution ( see figure 1 ) i.e. 2.5% or 0.25 in the upper tail and 2.5% or 0.25 in the upper tail and 2.5% or 0.25 in the lower tail since your hypothesis gives only a difference and not a direction. You will reject the null hypothesis on the basis that the sample mean falls into the area beyond 1.96 S.E. Otherwise if it falls into area 0.475 corresponds to 1.96 S.E. you can accept the null hypothesis.
Suppose you want to reduce the risk of committing a Type I error, reduce the size of the rejection region. If the hypothesis is treated at 1% i.e. 0.01 level of significance. If we consult the table of areas under the normal curve (table - 2), we find the acceptance region of 0.495 ( (one half of .99) is equal to 2.58 S.E. from mH i.e. z-score = 0.
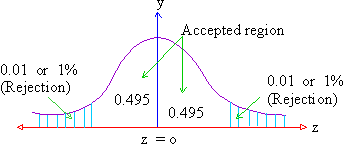
You will still reject the null hypothesis of no difference, if the class sample is either much higher or much lower than our population mean of 75.
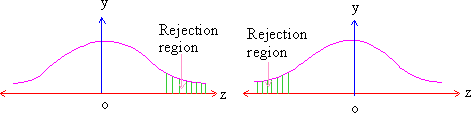
As distinguished from the two-tailed test, we can
apply a directional - one sided i.e. one-tailed test also because
in some cases it is necessary to guard against only small values
of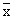 
(i.e. sample mean). One-tailed test is so called because the rejection
region will be located in only one-tail, which may either be on
the upper or the lower side of the distribution depending upon the
alternative ( Ha ) hypothesis formula. For example, we
want to test a hypothesis that the average income per household
is greater than $ 5000 against the alternative hypothesis that the
income is $ 1000 or more. We will place all a
risk on the upper-side of the theoretical sampling distribution
and the test will be one-tailed. On the other hand, if we are testing
that the average income per household is $ 5000 against Ha
that the income is less than $ 5000 or less, the a
risk is on the lower side of the distribution and the test will
be one sided.
Click here to enlarge
Summing up, if the population as specified mean say mo then the null hypothesis would be Ho : m = mo and alternative (researcher’s) hypothesis could be :
1) Ha : m ¹ mo
( i.e. m > mo
or m < mo
)
2) Ha : m
> mo
3) Ha : m
< mo
|
