8.10 Power Of A Hypothesis Test
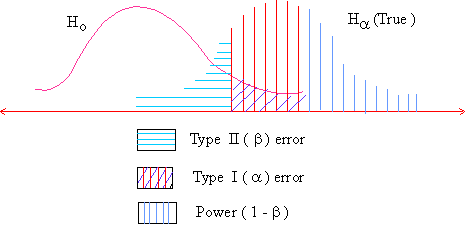
The measure of how well the test of hypothesis is working, is called the 'power of the test'. In hypothesis testing both a ( the probability of Type-I error) and b (the probability of Type II error) should be small.
Type I error occurs when we reject Ho which is true and a (the significance level of the test) is the probability of making type - I error. Once the significance level is fixed, nothing can be done about a. Type II error occurs when we accept Ho which is false. The probability of type II error is b. The smaller the value of b, the better is the test. Alternately ( 1 - b ) i.e. the probability of rejecting Ho when it is false should be as large as possible.
Rejecting Ho when it is false is exactly what a good test must do. A high value of (1 - b ), mostly close to 1, means that the test is working in high gear. A low value of (1 - b ), mostly close 0, means that the test is working poorly.
Thus (1 - b ) is the measure of
the power of the test. If we plot the values of ( 1 - b
) for each value of m f2 for
which Ha is true, the resulting curve
is known as a power curve.
You can see from the figure given below that the
power is simply ( 1 - b ). In testing
of a hypothesis high power is desirable. As we know that the Type
I error or a is usually set in advance by a researcher but the Type
II error or b for a given test is harder to know as it requires
estimation of the distribution of Ha, which is unknown
in most of the cases. So like b, the
power can be difficult to estimate accurately, but increasing the
sample size n, we can increase the power of the test.
Click here to enlarge
|